
18 Oct Glass Fracture Simulation
Computational Simulation of Johnson-Holmquist Glass Model
Numerical simulation of glass is complex and requires near exact physical properties and accurate computational modelling before its data can be trusted and extrapolated.Material property of a glass is attained through chemical adhesion under heat load. Its properly is effected by the chemical composition and spatial arrangement during thermal bonding and hence its failure is not pre-defined. Glass strength is dependent on various parameters such as chemical composition, void and flaws inclusion, surface roughness, specimen size and temperature etc.

Hence, computational method to simulate a perfect brittle fracture for glass is quite complex.
Simulation Case
A glass slab of 50mm thick is being shot with 0.5 cal. bullet where bullet velocity is assumed to be 2400m/s. The glass slab is an inertial mass which is restrained on the two sides only. Material is a generic glass model that exhibits the Johnson-Holmquist glass model and is sensitive to strain rates, plastic strains and pressure.

Result Summary
The simulation was done for relatively coarse meshing to demonstrate the brittle fracture scheme and model setup involved non-linear and transient effect and was simplified to save computation time. In the picture give below one can see the cavitation or a accumulated material damage is visible on the impact region of the glass slab.
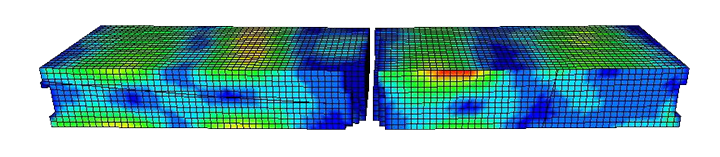
Cavitation or blown out material is evident due to high speed of the bullet which causes the damages to remain localized. However, if the velocity is lesser then the impact area would be large and blown out effect would be on a large span of glass slab. Further, the glass also breaks from the middle and side restraints that were modeled in the simulation. This is perhaps due to the brittle behavior of the glass, high impact loading and material self weight.
The most basic test is to analyze the drop in internal energy after collision and increase in glass velocity and kinetic energy after collision.
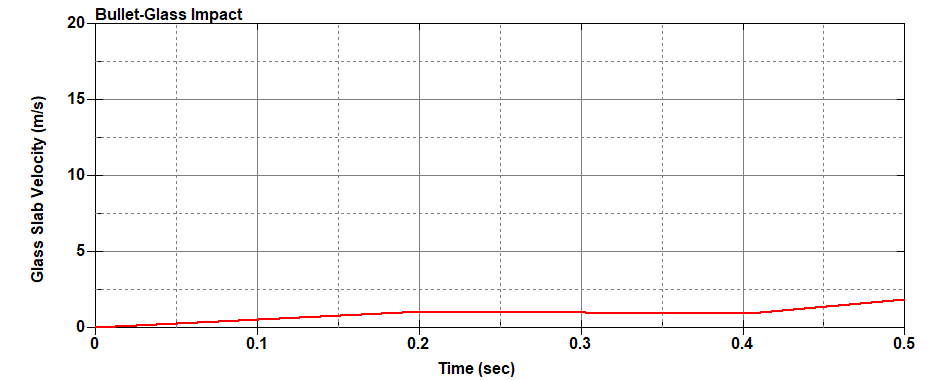
In the above graph, it is evident that a very high speed bullet hits the glass slab at a near zero second and induces small velocity increment. From 0-0.2 sec. the glass slab is under elastic strain limit and stabilizes from 0.2-0.3 sec. before falling freely under gravity at 0.4 sec.
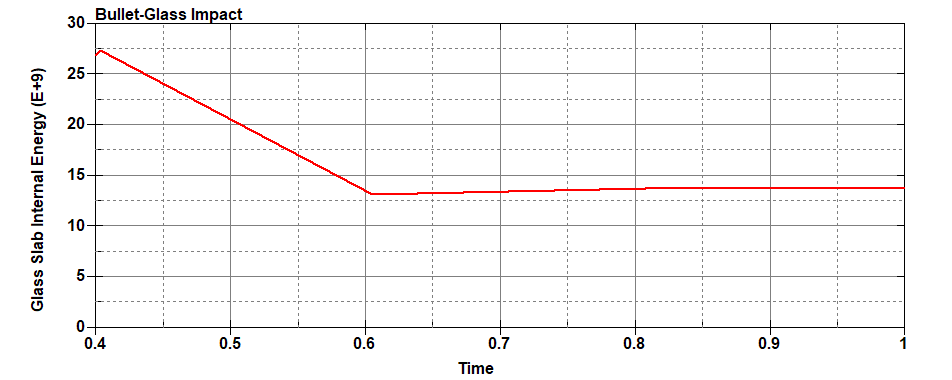
JH glass model indicates that during brittle fracture the net decrease in internal energy of glass sample is observed, which is evident from the above graph which shows fall in the internal energy after impact collision and brittle fracture.
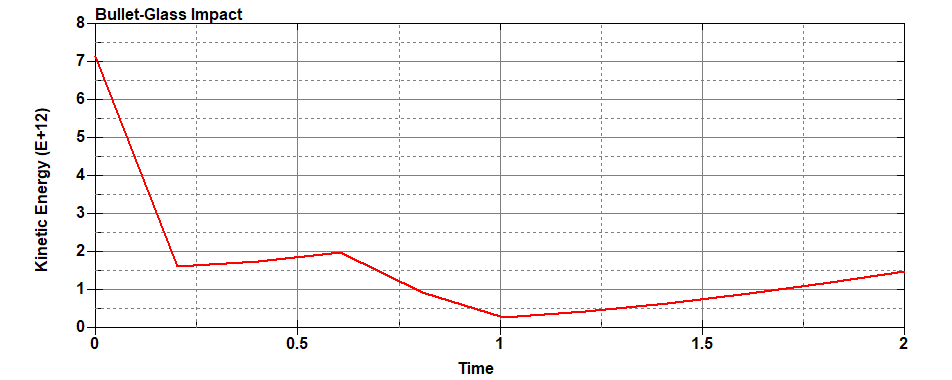
Kinetic energy history reveals the concise and more appropriate picture of the impact. The penetration of bullet is from 0-0.2 sec where it looses significant velocity. Decrease in KE at 1.0 sec could not be explained and may be assumed to be a associated with the computational error due to relatively coarse mesh size of FE model. However, the model addresses the macroscopic picture of the brittle fracture during the glass-bullet high speed impact.
However, there are other key relation that needs to be analyzed and ensured for the correctness of the simulation setup such as Strength vs Pressure for surface and interiors of glass slab, Penetration Velocity for the bullet and Pressure vs Volumetric Strains etc. These relations requires dense meshing for FE.




SEO Service
Posted at 16:26h, 01 FebruaryAwesome post! Keep up the great work! 🙂
AffiliateLabz
Posted at 21:52h, 15 FebruaryGreat content! Super high-quality! Keep it up! 🙂
Brianscogs
Posted at 20:02h, 29 MarchJust simply want to mention I am delighted I stumbled in your site.
Jamesrip
Posted at 07:23h, 27 AprilI value the content on your website. Thanks for your time.
ปั้มไลค์
Posted at 21:06h, 06 JulyLike!! Thank you for publishing this awesome article.